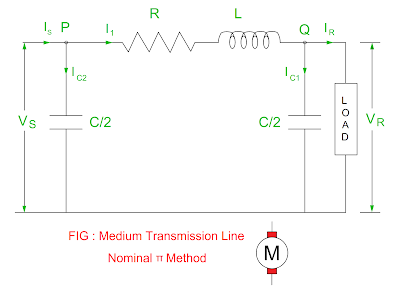
Medium Transmission Line: Nominal π method
The total capacitance of the transmission line is divided into two parts, half at the sending end side and another half at the receiving end side in the nominal π method. All the parameters are given considering three phase transmission line.
Let
VS =
Sending end voltage to neutral
VR =
Receiving end voltage to neutral
IS = Sending
end current
IR =
Receiving end current
IC1 =
Capacitance current at the receiving end side
IC2 =
Capacitance current at the sending end side
R = Resistance of
transmission line, resistance to the neutral in the three-phase line
X = Reactance of
transmission line, reactance to the neutral in the three-phase line
Z = R + j X = Total
impedance
Y = jXC
= Admittance
A, B, C and D =
Constant
Generalized
Constant of the transmission line is given by sending end voltage and sending
end current equation
VS = AVR
+ BIR……. ( 1 )
IS = CVR + DIR……....( 2 )
Nominal π method: ABCD Parameters
Apply KCL at point
Q,
I1 = IR
+ IC1
I1 = IR
+ ( Y/2 ) VR ……( 3 )
Apply KCL at point
P,
Is = I1
+ IC2
Is = I1
+ ( Y/2 ) Vs ………( 4 )
Substitute value
of I1 from equation ( 3 )
Is = IR
+ ( Y/2 ) VR + ( Y/2 ) Vs ………( 5 )
Sending end
voltage VS = VR + I1( Z )
Substitute value
of I1 from equation ( 3 )
VS = VR
+ { IR + ( Y/2 ) VR } ( Z )
= VR + Z IR + ( ZY/2
) VR
= VR + ( ZY/2 ) VR + Z IR
= ( 1 + ZY/2 ) VR + Z IR
VS = ( 1 + ZY/2 ) VR + Z IR ….. ( 6 )
Compare equation (
6 ) and ( 1 )
VS = AVR
+ BIR
VS = (
1 + ZY/2 ) VR + Z IR
Therefore A = ( 1 + YZ/2 ) and B = Z
From equation ( 5
)
Is = IR
+ ( Y/2 ) VR + ( Y/2 ) Vs
Substitute value
of Vs from equation ( 6 )
Is = IR
+ ( Y/2 ) VR + ( Y/2 ) {( 1 + ZY/2 ) VR + Z IR }
Is = IR
+ ( Y/2 ) VR + ( Y/2 + Y2Z/4 ) VR + ( YZ/2 ) IR
Is = (
Y/2 ) VR + ( Y/2 + Y2Z/4 ) VR + IR + ( YZ / 2 ) IR +
Is = {
Y/2 + Y/2 + Y2Z/4 ) VR +
{ 1 + ( YZ / 2 ) } IR
Is = {
Y + Y2Z/4 ) VR + {
1 + ( YZ / 2 ) } IR
Is = { 1 + ( YZ / 2 ) } IR +
Y ( 1 + Y2Z/4 ) VR ….. ( 7 )
Compare equation (
7 ) and ( 2 )
IS = CVR
+ DIR
Is = Y
( 1 + YZ/4 ) VR + { 1 + ( YZ / 2 ) } IR
Therefore C = Y ( 1 + YZ/4 ) and D = 1 + ( YZ / 2 )
From the above
value of A, B, C and D
A = ( 1 + YZ/2 )
B = Z
C = Y ( 1 + YZ/4 )
D = 1 + ( YZ / 2 )
Therefore
AD – BC = ( 1 + YZ/2 ) × ( 1 + YZ/2
) – Z × Y ( 1 + YZ/4 )
= ( 1 + YZ + Y2Z2/4 ) – YZ – Y2Z2/4
= 1
|
You
may also like to read these articles : |







No comments:
Post a Comment