High Pass Butterworth Filter

In this article, details study of first order high pass Butterworth filter, its frequency response, voltage gain, and second order high pass Butterworth filter is given.

First order High Pass Butterworth Filter

• The high pass filter is obtained by changing frequency determining component – resistors and capacitors in the low pass filter. 
• The first order high pass filter is obtained by interchanging R and C in the first order low pass filter. 
• Figure shows first order high pass Butterworth filter.

Lower cut off frequency

• It is frequency at which gain of the amplifier reduces from maximum to 70.7% of its maximum value. 
• It is from frequency response graph, one can say that lower cut off frequency is determining parameter for stop band frequencies and pass band frequencies.

Impedance of the capacitor = – jX_C

                                            = – j ( 1 / ωC )

                                            = – j / 2πfC

                                            = 1 / j2πfC

Input voltage at point P according to voltage divider rule

V_P = V_in { R / ( R – jX_C ) }

     = V_in { R / ( R + 1 / j2πfC  ) }

     = V_in { R / (( j2πfRC + 1) / j2πfC  ) }

     = V_in { j2πfRC / ( 1 + j2πfRC ) }

Let us consider that

Lower cut off frequency f_L = 1 / 2πRC

Divide numerator and denominator by 1 /2πRC

        = V_in { ( jf ) / ( 1 / 2πRC ) +( j2πfRC / 2πRC )

        = V_in { jf / ( 1 / f_L + jf ) }

        = V_in { jf / ( 1 +jf_L f ) / f_L }

        = V_in { jf f_L / ( 1 + jf_L f ) }

Divide numerator and denominator by f_L²

         = V_in { j( f / f_L ) / ( 1 + j( f / f_L )  }

Output voltage V_o = A_F V_P

Where A_F = gain of the OP – Amp 

                 = ( 1 + R_F / R₁ )

Output voltage V_o = A_F V_P

                 = ( 1 + R_F / R₁ ) { j( f / f_L ) / ( 1 + j( f / f_L ) } V_in

Voltage Gain: V_o / V_in = ( 1 + R_F / R₁ ) { j( f / f_L ) / ( 1 + j( f / f_L ) }

Magnitude of Voltage Gain: ( 1 + R_F / R₁ ) { ( f / f_L ) / ( 1 + √ ( f / f_L )² }

                                          = A_F{ ( f / f_L ) / ( 1 + √ ( f / f_L )² }

 

Frequency response of high pass Butterworth filter

 

 

• When the frequency decrease that of lower cut off frequency, the high pass Butterworth filter rolls at – 20 dB / dec. 
• The voltage gain reduced to 0.707A_F at lower cut off frequency. 
• The voltage gain becomes constant when frequency increases beyond lower cut off frequency.

Frequency	Voltage gain
Low frequency	< AF
Lower cut off frequency	= 0.707AF
Greater than lower cut off frequency	Constant

 

Second order High Pass Butterworth Filter

• The second order high pass Butterworth filter can be obtained by interchanging frequency determining components R & C in the second order low pass filter. 
• The second order high pass Butterworth filter is shown in the Figure.

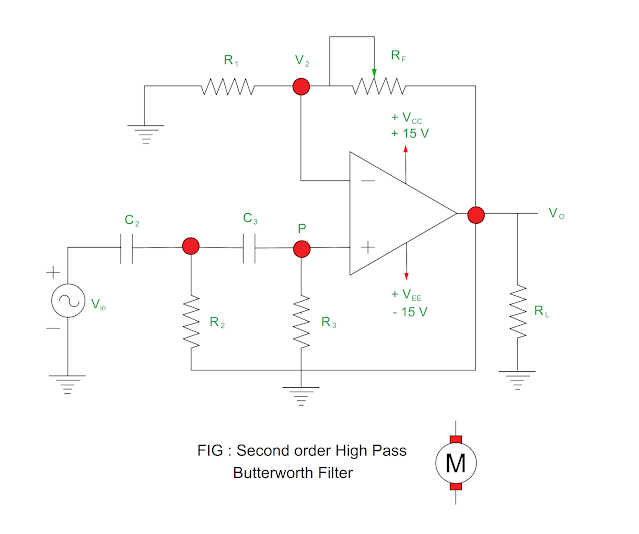
Magnitude of Voltage Gain: A_F / √ { 1 + ( f_L / f )² }

Where

    f = Input frequency

   f_L = Low cut off frequency

        =  1 / 2π √ ( R₂ ) ( R₃ ) ( C₂ ) ( C₃ )

  A_F = Pass band gain

You may also like :

Types of Filter Circuit

What is Mobility?

Power & Energy

Potential & Potential Difference